[BOJ][C++] 백준 17404번 RGB거리 2

17404번 RGB거리 2

1. 문제 정보

백준 온라인 저지 [17404번 RGB거리 2] 문제의 링크입니다.

문제

RGB거리에는 집이 N개 있다. 거리는 선분으로 나타낼 수 있고, 1번 집부터 N번 집이 순서대로 있다.

집은 빨강, 초록, 파랑 중 하나의 색으로 칠해야 한다. 각각의 집을 빨강, 초록, 파랑으로 칠하는 비용이 주어졌을 때, 아래 규칙을 만족하면서 모든 집을 칠하는 비용의 최솟값을 구해보자.

• 1번 집의 색은 2번, N번 집의 색과 같지 않아야 한다.
• N번 집의 색은 N-1번, 1번 집의 색과 같지 않아야 한다.
• i(2 ≤ i ≤ N-1)번 집의 색은 i-1, i+1번 집의 색과 같지 않아야 한다.

입력

첫째 줄에 집의 수 N(2 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 각 집을 빨강, 초록, 파랑으로 칠하는 비용이 1번 집부터 한 줄에 하나씩 주어진다. 집을 칠하는 비용은 1,000보다 작거나 같은 자연수이다.

출력

첫째 줄에 모든 집을 칠하는 비용의 최솟값을 출력한다.

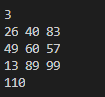
예제 입력1

3
26 40 83
49 60 57
13 89 99

예제 출력1

110

시간 / 메모리 제한

0.5초 / 128MB

---

2. 생각

1. 문제 1149번 RGB거리와 상당히 비슷한 문제였습니다. 이 문제는 문제 1149번 문제에 첫번째 집과 마지막 집의 색깔이 같으면 안된다는 제약조건이 추가되었습니다. i번째 집의 색깔이 i-1번째 집과 i+1번째 집의 색깔과 같으면 안된다는 조건은 아래의 링크를 참조해주세요.

   • https://minyeok2ee.gitlab.io/boj/boj-1149

2. 다이나믹 프로그래밍 문제는 큰 문제를 작은 문제로 쪼갤 수 있고 작은 문제의 정답을 통해 큰 문제의 정답을 구해나가는 방식을 사용합니다. 다이나믹 프로그래밍 코딩 방식 중 Bottom-up 방식은 i를 작은 문제부터 시작하여 n까지 늘려가며 답을 구하는 것이기 때문에 dp배열의 i 인덱스의 값을 구할 때 i-1인덱스의 값을 참조하는 경우가 대부분입니다.

3. 그런데 이 문제는 마지막 값이 처음의 값에 따라 구하는 방식이 달라져야합니다. 따라서 첫번째 집의 색깔을 정해놓고 시작합니다. 세 번 반복하며 처음에는 첫번째 집이 빨강색, 다음에는 첫번째 집이 초록색, 마지막에는 첫번째 집이 파랑색입니다.

4. i=0일 때는 첫번째 집이 빨간색, 1일 때는 첫번째 집이 초록색, 2일 때는 첫번쨰 집이 파랑색입니다.

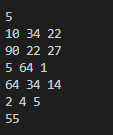
   i	k	dp[k][0] (빨강)	dp[k][1] (초록)	dp[k][2] (파랑)
   0	0	26	infinite	infinite
   	1	49 + infinite	60 + 26 = 86	57 + 26 = 83
   	2	13 + 83 = 96	89 + 83 = 172	99 + 86 = 185
   1	0	infinite	40	infinite
   	1	49 + 40 = 89	60 + infinite	57 + 40 = 97
   	2	13 + 97 = 110	89 + 89 = 178	99 + 89 = 188
   2	0	infinite	infinite	83
   	1	49 + 83 = 123	60 + 83	57 + infinite
   	2	13 + 143 = 156	89 + 123 = 212	99 + 123 = 222

5. 위의 표에 알고리즘이 동작하는 방식을 정리했습니다. 여기서 최소값은 96입니다.
   그러나 i가 0일 때, 최소값 dp[2][0] = 96은 첫번째 집과 마지막 집이 빨간색이므로 조건을 만족할 수 없습니다.
   따라서 i가 1일 때 최소값 dp[2][0] = 110이 답입니다.

---

3. 소스코드 (C++)

---

터미널의 입출력 화면 예제1

터미널의 입출력 화면 다른 예제1