[BOJ][C++] 백준 11052번 카드 구매하기
Updated:
11052번 카드 구매하기
1. 문제 정보
백준 온라인 저지 [11052번 카드 구매하기] 문제의 링크입니다.

문제
요즘 민규네 동네에서는 스타트링크에서 만든 PS카드를 모으는 것이 유행이다.
PS카드는 PS(Problem Solving)분야에서 유명한 사람들의 아이디와 얼굴이 적혀있는 카드이다. 각각의 카드에는 등급을 나타내는 색이 칠해져 있고, 다음과 같이 8가지가 있다.
- 전설카드
- 레드카드
- 오렌지카드
- 퍼플카드
- 블루카드
- 청록카드
- 그린카드
- 그레이카드
카드는 카드팩의 형태로만 구매할 수 있고, 카드팩의 종류는 카드 1개가 포함된 카드팩, 카드 2개가 포함된 카드팩, … 카드 N개가 포함된 카드팩과 같이 총 N가지가 존재한다.
민규는 카드의 개수가 적은 팩이더라도 가격이 비싸면 높은 등급의 카드가 많이 들어있을 것이라는 미신을 믿고 있다. 따라서, 민규는 돈을 최대한 많이 지불해서 카드 N개 구매하려고 한다. 카드가 i개 포함된 카드팩의 가격은 Pi원이다.
예를 들어, 카드팩이 총 4가지 종류가 있고, P1 = 1, P2 = 5, P3 = 6, P4 = 7인 경우에 민규가 카드 4개를 갖기 위해 지불해야 하는 금액의 최댓값은 10원이다. 2개 들어있는 카드팩을 2번 사면 된다.
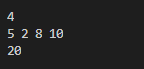
P1 = 5, P2 = 2, P3 = 8, P4 = 10인 경우에는 카드가 1개 들어있는 카드팩을 4번 사면 20원이고, 이 경우가 민규가 지불해야 하는 금액의 최댓값이다.
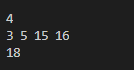
마지막으로, P1 = 3, P2 = 5, P3 = 15, P4 = 16인 경우에는 3개 들어있는 카드팩과 1개 들어있는 카드팩을 구매해 18원을 지불하는 것이 최댓값이다.
카드 팩의 가격이 주어졌을 때, N개의 카드를 구매하기 위해 민규가 지불해야 하는 금액의 최댓값을 구하는 프로그램을 작성하시오. N개보다 많은 개수의 카드를 산 다음, 나머지 카드를 버려서 N개를 만드는 것은 불가능하다. 즉, 구매한 카드팩에 포함되어 있는 카드 개수의 합은 N과 같아야 한다.
입력
첫째 줄에 민규가 구매하려고 하는 카드의 개수 N이 주어진다. (1 ≤ N ≤ 1,000)
둘째 줄에는 Pi가 P1부터 PN까지 순서대로 주어진다. (1 ≤ Pi ≤ 10,000)
출력
첫째 줄에 민규가 카드 N개를 갖기 위해 지불해야 하는 금액의 최댓값을 출력한다.
예제 입력1
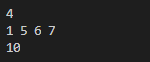
4
1 5 6 7
예제 출력1
10
예제 입력2
5
10 9 8 7 6
예제 출력2
50
예제 입력3
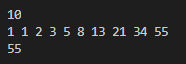
10
1 1 2 3 5 8 13 21 34 55
예제 출력3
55
예제 입력4
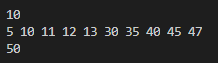
10
5 10 11 12 13 30 35 40 45 47
예제 출력4
50
예제 입력5
4
5 2 8 10
예제 출력5
20
예제 입력6
4
3 5 15 16
예제 출력6
18
시간 / 메모리 제한
1초 / 256MB
2. 생각
-
카드 n개를 구매할 때 최대 비용을 구하는 문제입니다. 큰 문제 카드 n개를 구매할 때 최대 비용을 두하는 것은 카드 1개, 2개, … n-1개를 구매할 때 최대 비용을 구하는 작은 문제로 쪼갤 수 있고, 작은 문제의 답을 이용해 큰 문제의 답을 풀 수 있으므로 다이나믹 프로그래밍 방법을 이용하여 문제를 풀겠습니다.
-
dp배열을 이용할 때 각 원소의 값에는 카드 i개를 구매할 때 드는 최대 비용으로 정의하겠습니다. 이것은 문제의 크기를 각 원소별로 줄인 것입니다. 카드 i개를 구매할 때의 방법은 카드 i개가 들어있는 팩을 1개 사거나, 카드 n-i개 들어있는 팩과 i개 들어있는 팩을 사면 됩니다.
-
i와 dp배열(인덱스별로 각 인덱스 개의 카드를 구매할 때 최대 비용), price배열(인덱스별로 각 인덱스 개의 카드를 구매할 때 드는 비용)을 이용하여 i를 증가시키며 dp배열을 1부터 차례로 채워가겠습니다.
예제 1의 예)
price 배열
1개 구매시 2 3 4 1원 5 6 7 dp 배열
i j i-j dp[i] = dp[i-j] + price[j] 1 1 1 - 1 = 0 dp[1] + price[0] = 0+1 = 1 2 1 2 - 1 = 1 dp[1] + price[1] = 1+1 = 2 2 2 - 2 = 0 dp[0] + price[2] = 0+5 = 5 3 1 3 - 1 = 2 dp[2] + price[1] = 5+1 = 6 2 3 - 2 = 1 dp[1] + price[2] = 1+5 = 6 3 3 - 3 = 0 dp[0] + price[3] = 0+6 = 6 4 1 4 - 1 = 3 dp[3] + price[1] = 6+1 = 7 2 4 - 2 = 2 dp[2] + price[2] = 5+5 = 10 3 4 - 3 = 1 dp[1] + price[3] = 1+6 = 7 4 4 - 4 = 0 dp[0] + price[4] = 0+7 = 7 dp배열을 각 원소만큼의 카드를 구매하는데 드는 최대 비용으로 정의했습니다.
그러므로 dp[i] = dp[i-j] + price[j]에서 dp[i]의 값이 dp[i-j] + price[j]의 값보다 클 때는 업데이트할 필요는 없습니다. 따라서 max 함수를 사용했습니다.
3. 소스코드 (C++)